超薄3D-IC封裝在制造過程和溫度循環測試耦合負載影響下的可靠性評估-深圳市福英達


超薄3D-IC封裝在制造過程和溫度循環測試耦合負載影響下的可靠性評估
為應對物聯網和智能制造,基于摩爾定律的半導體芯片結構設計涉及相關電子元器件尺寸的縮小。因此,晶體管的密度逐漸增加。為實現上述封裝要求,解決傳統封裝框架的瓶頸,現有研究以堆疊方向的三維互連為主流技術。關鍵技術是硅通孔 (TSV) 和焊料微凸塊 (μbump) 的互連,這通常是失效位置方面的關注領域。三維集成電路(3D-IC)封裝在制造工藝和可靠性方面的諸多挑戰需要克服,其中加速熱循環測試(TCT)的可靠性問題尤為關鍵。根據 JESD22-A104D 規范,封裝組件之間的劇烈熱膨脹系數(CTE) 不匹配會在熱負載下對關鍵焊料 μbump 產生明顯的熱應力 。
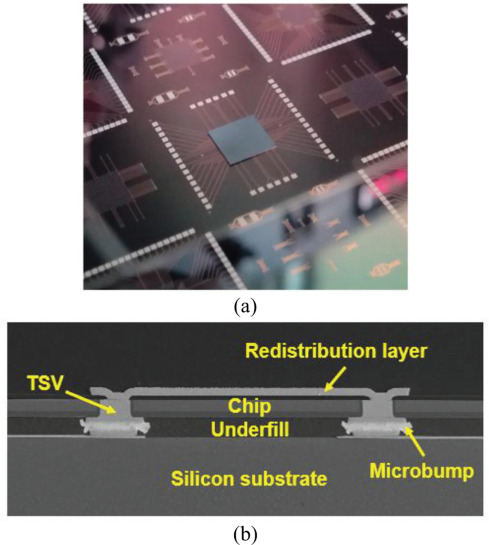
圖 1. 實際超薄型芯片3D-IC封裝
Garofalo-Arrhenius蠕變模型
當材料在高于熔點 0.5 T m的溫度下承受固定載荷時,應變隨時間增加。這種現象稱為蠕變。圖 2表明,韌性材料在固定應力和溫度下的蠕變行為可分為三個階段,即初級、二級和三級蠕變。穩態區占蠕變變形的大部分。對于應用于電子封裝的焊點,Garofalo-Arrhenius 模型,也稱為雙曲正弦模型,被廣泛用于定義蠕變行為。圖 2所示的第二階段呈現穩態蠕變,由 Garofalo-Arrhenius 模型描述。
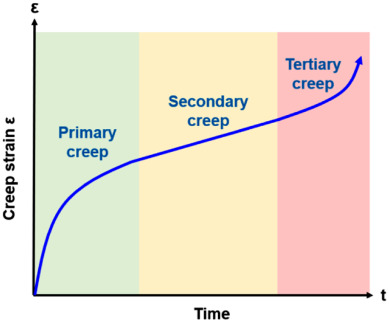
圖2. 固定應力下焊料合金蠕變應變與時間的關系。
表1列出了本 FEA 中使用的詳細材料屬性。為了準確預測 SnAg μbump 的蠕變行為和封裝翹曲,我們將非線性材料屬性分配給焊料和銅 [ 34 ]。焊料表現出與溫度相關的特性和蠕變行為。表 2列出了 SnAg 焊料的 Garofalo–Arrhenius 蠕變模型的系數。由于熱循環負荷的最高溫度(125℃)超過成型材料的玻璃化轉變溫度(Tg)(110℃),成型材料的楊氏模量大大降低,從而影響了成型材料的機械性能整個包裹。因此,在目前的 FEA 中,應考慮 Tg 作為成型材料。
表 1.當前 3D-IC 封裝 FEA 中使用的材料屬性列表。
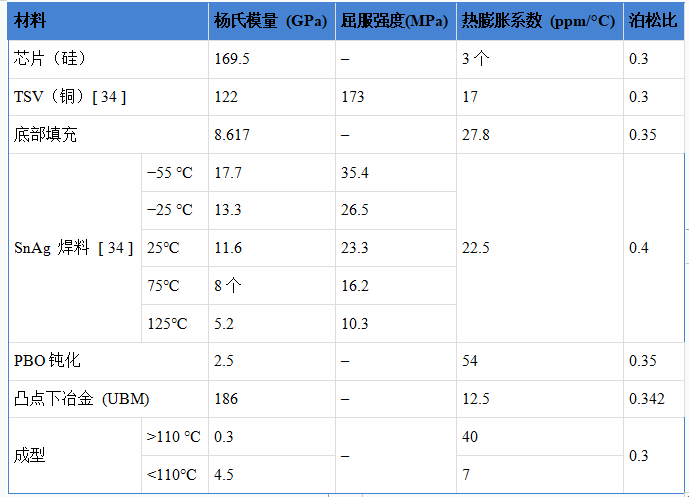
表 2. 96.5Sn3.5Ag 焊料的 Garofalo–Arrhenius 模型參數 [ 32 ]。

由于相關組裝過程中的巨大溫度變化,往往會在封裝結構內誘發對可靠性產生相當大影響的殘余應力。在這項研究中,通過闡明所提出的耦合載荷的問題和影響,預測了 TCT 之前封裝設備的實際機械狀態。 3D-IC封裝的超薄芯片制造工藝是將填充銅的 TSV 芯片粗磨至 100 μm,并調整其與硅基板的連接。在 250 °C 的熱壓下,芯片和基板粘合在一起,形成 15 μm 的間隙,然后通過毛細管作用填充底部填充材料。此后,在芯片上涂上較厚的成型材料,以分散芯片的磨削載荷,從而避免在將 100 μm 厚的芯片進一步磨削至 10 μm 厚度時發生芯片斷裂。然后將鈍化層沉積在組裝芯片的頂面上。由于相對于 TCT 持續時間的時間限制,在制造過程的模擬中忽略了 μbumps 的蠕變行為。本文采用的 TCT 條件遵循 JEDEC 標準 JESD22-A104 條件 D。溫度范圍介于 ?40 °C 和 125 °C 之間。從 25 °C 的室溫加熱到 125 °C 需要 450 秒。然后將 125 °C 的溫度保持 900 秒。溫度隨后在 900 秒內從 125 °C 降至 -40 °C。最終,溫度在 450 秒內恢復到 25°C。一次 TCT 持續 3600 秒。在這項工作中,在 FEA 中執行了七個完整的 TCT,以獲得關鍵焊料 μ 凸塊的收斂、增量和等效塑性和蠕變應變。
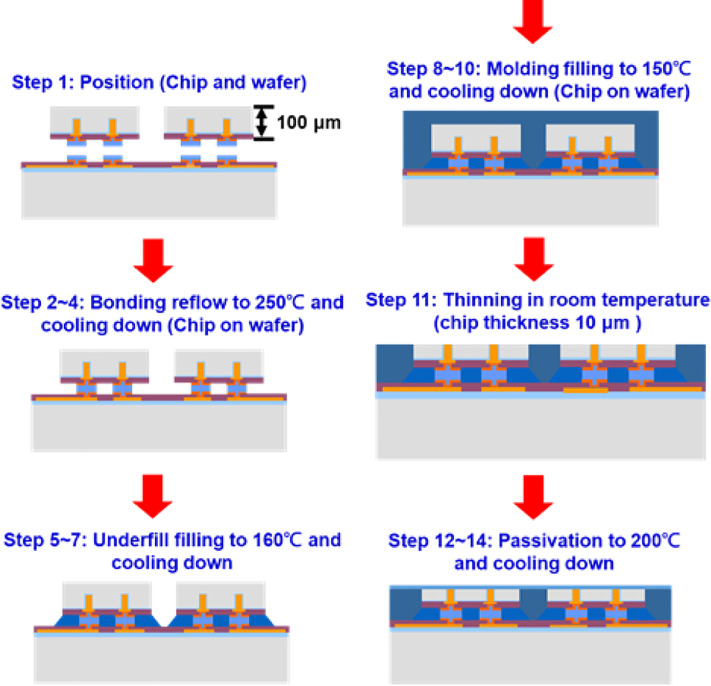
圖 5. 所提出的 3D-IC 封裝超薄芯片的制造工藝示意圖。
圖 6顯示了制造過程和 TCT 的耦合載荷影響的增量和等效塑性和蠕變應變。峰值應變出現在溫度恢復到室溫的過程的后期,因為此時在封裝組件中引入了最顯著的CTE失配。以第 12 步的情況為例,其中結構剛度因切屑變薄而降低。當封裝加熱到 200 °C 時,估計會出現明顯的增量塑性應變峰值和等效塑性應變峰值。此外,分析結果表明,在七次 TCT 之后,μbumps 的增量和等效蠕變應變幾乎與它們的增量和等效塑性應變相同。因此,在評估 TCT 的可靠性時,不能忽視 SnAg 焊料 μbumps 的蠕變效應。圖 7顯示了整個封裝結構在每個制造步驟和 TCT 中的翹曲變化。第 12 步的嚴重翹曲可歸因于臨界變形的增加,該變形引起相應的增量和等效塑性應變。此外,TCT 相對于制造部分引起的翹曲變化相當小。也就是說,在后續TCT的可靠性評估中需要考慮制造過程中殘余應力的影響。

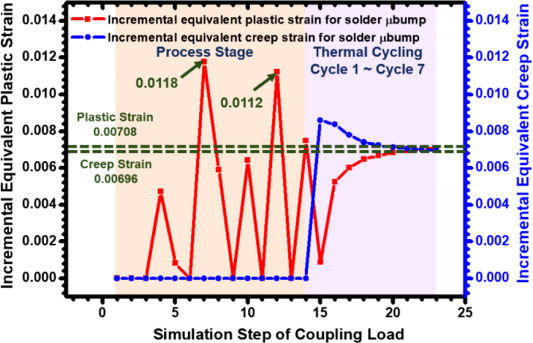
圖 6.TCT的耦合載荷下,最外層焊料 μbumps 的估計等效塑性和蠕變應變增量的變化。

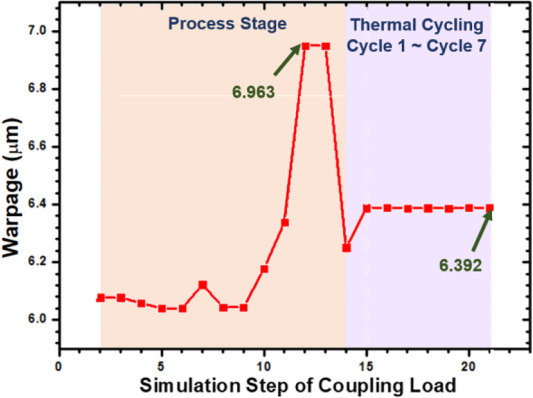
圖 7.基于所提出的仿真方法的預測, 3D-IC 封裝的超薄芯片在處理步驟和后續TCT下的翹曲變化。
5.1.組裝芯片厚度
如圖8所示。隨著切屑厚度增加到大于 ~20 μm,應變增量增加。這種現象隨著使用具有高楊氏模量的底部填充材料而變得廣泛。在 20 和 50 μm 之間的芯片厚度過渡處,芯片顯示出最小的結構彈性性。因此,影響 μbump 可靠性的主要機制是底部填充材料和 PBO 材料之間的 CTE 不匹配。然而,隨著采用剛性厚度層,填充銅的 TSV 與芯片之間的熱失配會增加。因此,在制造過程和 TCT 的負載下,μbumps 會積累并維持較大的剪切應變。這種情況導致非彈性應變增加。相比之下,當具有低楊氏模量的底部填充物用作應力緩沖層以分散μbump的剪切變形時,可以減少μbump的應變增量。


圖 8.考慮具有不同楊氏模量值的底部填充時,芯片厚度對臨界 μbump 上等效非彈性應變增量的依賴性。
5.2.TSV間距效應
如圖 9所示當 TSV 間距從 170 μm 擴展到 250 μm 時,等效非彈性應變增量略有下降。原因可以歸因于這樣一個事實,即不同材料之間的 CTE 不匹配引起的應變可以均勻地分布到每個焊料 μbump。然而,隨著應用各種底部填充物,觀察到應變幅度的顯著差異。結果表明,在保持相同間距的情況下,具有較低底部填充楊氏模量的 μbump 的應變增量會減小。因此,設計的參數,即底部填充的楊氏模量,在減小 μbump 應變方面比 TSV 間距更敏感。分析結果表明,具有 0.3 GPa 楊氏模量的底部填充是減少臨界 μbump 應變累積的良好選擇。

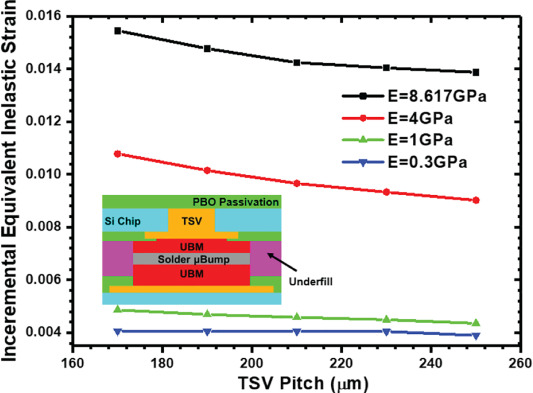
圖9. 底部填充膠的四種不同楊氏模量被考慮時, TSV 間距對 μbump 非彈性應變增量的依賴性。
5.3.TSV半徑效應
對于TSV半徑的參數化分析,估計結果如圖10所示。與之前關于其他參數的討論類似,當 TSV 的半徑尺寸固定時,底部填充膠的低楊氏模量會導致 μbump 的應變增量較低。 TSV 半徑的增加通常會導致較大的應變增量。盡管如此,具有 25 μm TSV 半徑和楊氏模量為 4 和 8.617 GPa 的底部填充的組裝芯片降低了 μbump 應變。因此,估計結果表明 TSV 半徑與 μbump 的應變增量有關。當 TSV 半徑從 10 μm 擴展到 25 μm 時,與 PBO 材料的接觸面積也會擴大。由于封裝組件之間的 CTE 不匹配導致的嚴重變形會增加 μbump 應變。除了凸點下冶金層(UBM)外,還包裹焊料 μbump 的底部填充物具有較低的楊氏模量,可提高結構的柔韌性。因此,可以大大降低上述應變。當 TSV 半徑為 25 μm 時,連接在焊料 μbump 上方的 UBM 層具有相同的直徑,并且 μbump 內的應變也會增加。使用楊氏模量為 4.0 或 8.617 GPa 的底部填充膠可以有效地抵抗 μbump 應變。因此,研究了 μbump 應變增量的下降。與楊氏模量為 0.3 或 1 的底部填料的觀察結果相反,楊氏模量為 4.0 或 8.617 GPa 的底部填料抑制封裝翹曲的能力非常有限,盡管此時仍可以釋放 μbump 應變。因此,最終應變略有增加。
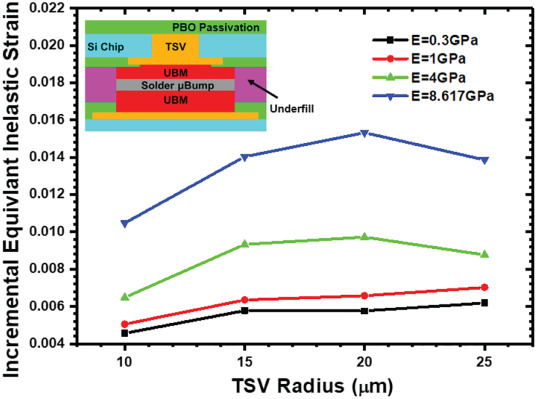
圖 10. 當考慮底部填充的幾個楊氏模量時,TSV 半徑對 μbump 非彈性應變增量的依賴性。
結論
分析結果表明,由于溫度相對于TCT溫度的劇烈變化,封裝結構在加工階段發生了嚴重的翹曲。在 TCT 之前幾乎達到會聚扭曲。此外,在制造過程中,塑性應變會在焊料 μbump 內大量累積。這種情況導致 TCT 期間塑料積累的減少。盡管如此,應考慮蠕變行為,因為 μbump 的蠕變應變通過 TCT 載荷達到其自身非彈性應變累積的一半。
關于參數分析,估計結果表明,相對較薄的芯片可以獲得良好的結構柔韌性,以釋放焊料 μbump 的應變。延長 TSV 間距也有利于分散傳輸到 μbump 的 CTE 失配變形,從而獲得低應變增量。至于 TSV 半徑,發現較大的半徑會導致填充銅的 TSV 和 PBO 層之間的接觸面積增加。因此,臨界 μbump 的應變增加主要是因為封裝材料的嚴重 CTE 變形。此外,選擇具有低楊氏模量的底部填充材料,被視為一種應力緩沖機制,是滿足焊料μbumps可靠性要求的好方法。
深圳市福英達能夠生產潤濕性優秀的超微錫膏產品(T6及以上),能夠適用于各種表面處理的PCB上。不僅于此,福英達錫膏的粒度分布區間窄,抗坍塌性能好且焊后機械強度高。歡迎客戶與我們合作。


參考文獻
Chang-Chun Lee, Yu-Min Lin, Hou-Chun Liu, Ji-Yuan Syu, Yuan-Cheng Huang & Tao-Chih Chang(2021). Reliability evaluation of ultra thin 3D-IC package under the coupling load effects of the manufacturing process and temperature cycling test. Microelectronic Engineering, vol. 244-266.








 返回列表
返回列表



